无论是科学研究还是统计调查,显著性检验作为判断两个或是多个数据集之间是否存在差异的方法一直被广泛应用于各个科研领域。
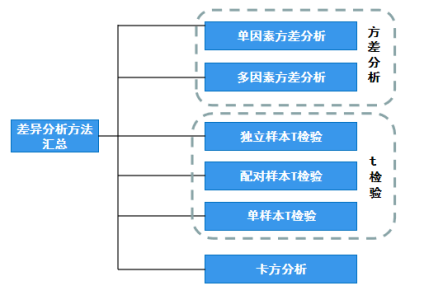
针对不同的数据类型,研究者需要使用不同的方法和统计量来实现具体的差异性研究问题。差异研究通常包括以下几类分析方法,分别是T检验、方差分析和卡方检验。
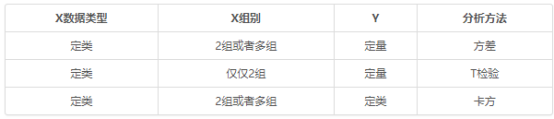
其实核心的区别在于:数据类型不一样。如果是定类和定类,此时应该使用卡方分析;如果是定类和定量,此时应该使用方差或者T检验。
方差和T检验的区别在于,对于T检验的X来讲,其只能为2个类别比如男和女。如果X为3个类别比如本科以下,本科,本科以上;此时只能使用方差分析。
进一步细分
1)方差分析
根据X的不同,方差分析又可以进行细分。X的个数为一个时,我们称之为单因素方差;X为2个时则为双因素方差;X为3个时则称作三因素方差,依次下去。当X超过1个时,统称为多因素方差。
单因素方差分析的基本思想:变异分解、总变异=随机变异处理因子变异,总变异=组内变异。F=组间变异/组内变异,f值越大,处理因子的影响越大。
2.2单因素方差分析使用前提的独立性:不满足独立性会有很大影响。因为信息中有“重叠”的部分
疑问:在哪里可以验证?卡片检查?卡方检验了两个分类变量
正规性:对正规性的要求稳健
方差一致性:检测方法除levene’s检测外,还用于Bartleet法(比较各组方差的加权算术平均数和几何平均数)、Hartley法)、Cochran法)样本量相同的情况)。
方差分析对变量的类型有要求吗?需要分析的都是连续变量
2.3如果不满足单因素法分析的使用前提(变换方法对数变换、平方根变换、平方根反正弦变换、平方变换、倒数变换、框-Cox变换(分段函数) ) ) ) ) ) ) ) ) ) ) ) ) )。
2.4单因素方差分析的应用场景t检验只能检验两组样本的平均数差。对于多组样品,需要采用方差分析;
操作:分析—均值—均值比较预分析,可以粗略看出各均值是否相同,方差是否均匀;进行开放分析—比较均值—单因素anova;
应用场景(平均数量之间的多重比较)全双工比较)、每组的平均数量的精细比较(可以指定要比较的两组并设置系数)、组之间的平均数量趋势检查)。拟合线性或非线性模型以利用组变量中出现的顺序信息
2.5方差分析结束后,若均值不同,可进行两种比较(预比较、后比较) LSD法),用于预规划比较,最为灵敏;检查水平未校正,每次为
Sidak法:第二敏锐;
Bonferroni法:用于预先规划的比较,第三敏锐;
Scheffe法:多数样品含量不同时,第四锐敏;
Dunnett法:常用于多个实验组与一个对照组的比较,第五敏锐;
如何查找同质子组:
S-N-K法:将所有样本分为多个子集;
Tukey法:任意两组比较,要求样品含量相同,MEER不超过;
Duncan法:与SNK法相似;
评论:
CER :每次进行比较都会犯错误的概率;
ERC )在完全无效的假设下,完成所有比较后犯一种错误的概率;
MEER (在部分或完全假设下,犯某种错误的最大概率值,即最大实验误差率。
疑问:单因素方差分析的先验和后验有什么区别,为什么结果不同?
多因素方差分析通常用于类实验式问卷研究。
在方法选择上,问卷研究通常会使用方差分析,但某些专业,比如心理学、教育学或者师范类专业等涉及到实验研究时,更多会使用T检验进行分析,另外方差分析与T检验还有较多差异,在某些分析中只能使用其中一种。
2)T检验
T检验共分为三种方法,分别是独立样本T检验,配对样本T检验和单样本T检验。
独立样本T检验和单因素方差分析功能上基本一致,但是独立样本T检验只能比较两组选项的差异,比如男性和女性。相对来讲,独立样本T检验在实验比较时使用频率更高,尤其是生物、医学相关领域。针对问卷研究,如果比较的类别为两组,独立样本T检验和单因素方差分析均可实现,研究者自行选择使用即可。
独立样本T检验和配对样本T检验功能上都是比较差异,而且均是比较两个组别差异。但二者有着实质性区别,如果是比较不同性别,婚姻状况(已婚和未婚)样本对某变量的差异时,应该使用独立样本T检验。如果比较组别之间有配对关系时,只能使用配对样本T检验,配对关系是指类似实验组和对照组的这类关系。另外独立样本T检验两组样本个数可以不相等,而配对样本T检验的两组样本量需要完全相等,并且独立样本T检验与配对样本T检验时在SPSS的数据放置格式不同。
T检验的第三种分析方法为单样本T检验。比如问卷某题项选项表示为1分代表非常不满意,2分代表比较不满意,3分代表一般,4分代表比较满意,5分代表非常满意,当想分析样本对此题项的态度是否有明显的倾向,比如明显高于3分或者明显低于3分时,即可以使用单样本T检验。单样本T检验是比较某个题项的平均得分是否与某数字(例子是与3进行对比)有着明显的差异,如果呈现出显著性差异,即说明明显该题项平均打分明显不等于3分。此分析方法在问卷研究中较少使用,平均得分是否明显不为3分可以很直观的看出,而不需要单独进行检验分析。
单样本非参数检验
K-S检验:针对连续变量,考察是否符合正态分布
操作:打开–分析–非参数检验–单样本
二项分布检验:针对两分类变量,考察是否符合二项分布
操作:打开–分析–非参数检验–单样本
游程检验:考察总体的随机性
操作:打开–分析–非参数检验–单样本
两个独立样本的非参数检验(无效假设为两样本的中心位置是否相等)
Mann-Whitney U检验,两样本秩和检验,应用范围最广;
Kolmogorov-Smirnov Z检验:检验两个样本的累积频数分布曲线,判断两个样本的分布是否相同;
Moses Extreme Reactions 检验:Moses极端反应检验,单侧检验
Wald-Wolfowitz Runs 检验:单侧检验,无论是集中趋势、离散趋势、偏度的波动情况都能检测出来,如果只是检查中心位置,最好不用,检验两样本是否来自同样的分布;
操作:打开 分析—非参数检验—独立样本
多个独立样本的非参数检验
Kruskal-Wallis H检验(类似Wilcoxon符号秩检验,两样本在多样本上的推广)
中位数检验
Jonckheere-Terpstra检验:对连续变量和有序分类资料都使用,分组变量为有序分类资料时,检验效能要高于Kruskal-Wallis H检验
操作:打开 分析—非参数检验—独立样本
两个配对样本(求出差值,查看中位数是否为0,目的就是为了检验均值是否相等)
sign符号检验:只利用了符号信息,差值是否一半为正一半为负;
Wilcoxon符号秩检验:利用了符号和差值的大小顺序(符号 秩序)
操作:打开 分析—非参数检验—相关样本
多个相关样本非参数检验
Friedman 检验:基本思想是同区组的处理值和计算的秩比较才有意义,还附带齐性子集结果给出了准确的两两比较信息;
Kendall协和系数检验:为了检验各组评价是否一致,Friedman检验只能说明尚不能认为有差异,但是无法评判一致性,Kendall方法针对连续变量,
Cochran检验:有些评价只能用是否、好坏等二元数据来判断,Cochran只适用于二分类变量,用Kendall方法会有很多的打结现象。
操作:打开 分析–非参数检验–相关样本
通用方法—秩变换分析方法
前面有关秩的分析方法其实都是秩变换方法的不同应用,分析方法中可以直接将秩求出后再进行分析。
操作:转换 — 个案排秩(也可以指定生成符合正态分布的秩)
3)卡方分析
3.1卡方检验用于分析定类数据与定类数据之间的关系情况。例如研究人员想知道两组学生对于手机品牌的偏好差异情况,则应该使用卡方分析。卡方是通过分析不同类别数据的相对选择频数和占比情况,进而进行差异判断,单选题或多选题均可以使用卡方分析进行对比差异分析。
3.2 卡方检验的使用前提
最小期望频数均大于1
至少4/5的单元格期望频数大于5
计算时如果单元格期望频数小于5要和其他种类合并
样本观察值量超过50
3.3 卡方检验的使用目的
考察无序分类变量各水平在两组或多组间的分布是否一致;
检验某个连续变量的分布是否和理论分布一致;
分类变量的概率是否等于指定概率;
检验两个分类变量是否独立;
检验控制了其中几个因素后,剩余的两个分类变量是否独立;
检验两种方法的结果是否一致;
3.4 卡方检验的适用场景
单样本卡方检验
操作:打开 分析–非参数检验–单样本
两样本卡方检验
操作:打开 分析–描述统计–交叉表
两分类变量间关联程度的度量:定性描述两个分类变量是否存在关联(更为详细的可以根据相关分析)
操作:打开 分析–描述统计–交叉表
Kappa一致性检验(用于配对样本,如两个人针对一个事物的评价)
用于配对样本的检验,Kappa检验的结果是两个人的评价是否是相关的
操作:打开 分析–描述统计–交叉表
Mcnemar 配对卡方检验
Kappa检验只能看出两者是否有关联,但是不能判断是否一致,Mcnemar 配对卡方检验就可以解决两者是否一致的问题
操作:打开 分析–描述统计–交叉表
分层卡方检验
可以控制一个因素,如收入对车辆购买率的影响,可以将城市作为分层因素,从而可以得到更准确的结果,但是SPSS中只能进行两分类变量的检验,不能进行多分类的检验,且分层因素和要分析的因素之间如果存在交互关系也不能进行检验。
操作:打开 分析–描述统计–交叉表
来源:SPSSAU
版权说明:如非注明,本站文章均为 文译生物-专业的生物医学科研服务专家 原创,转载请注明出处和附带本文链接。